Intro to Stereo Vision

Stereo vision

The idea is to take a particular object and observe it from 2 slightly different viewpoints - in this way we get an understanding of shape from the idea of motion. Each eye (or camera) sees slightly different image.


Anaglyph stereo image - image resulted using encoding each eye’s image using filters of different colors, typically red and cyan.

E.g. if you put some blue filter on the image it will be blue. If you put some red filter on top - the resulted image will be dark.

Basic idea

  • Two images from two cameras taken under slightly different viewpoints (gif below).
  • Notable fact - parts in front go in particular way (on the left) and the parts in the
  • From 2 different viewpoints we get a sense of how the parts move (back or forth).

via Gfycat

Geometry of stereo

  • Cameras are defined by their optical centers.
  • 2 cameras are looking at some scene point.
  • If we can figure out what are 2 points in 2 cameras are the same scene point.

  • Furthermore, if I can figure out which way the cameras are pointed, we can figure out the depth of that point (arrow in the image).

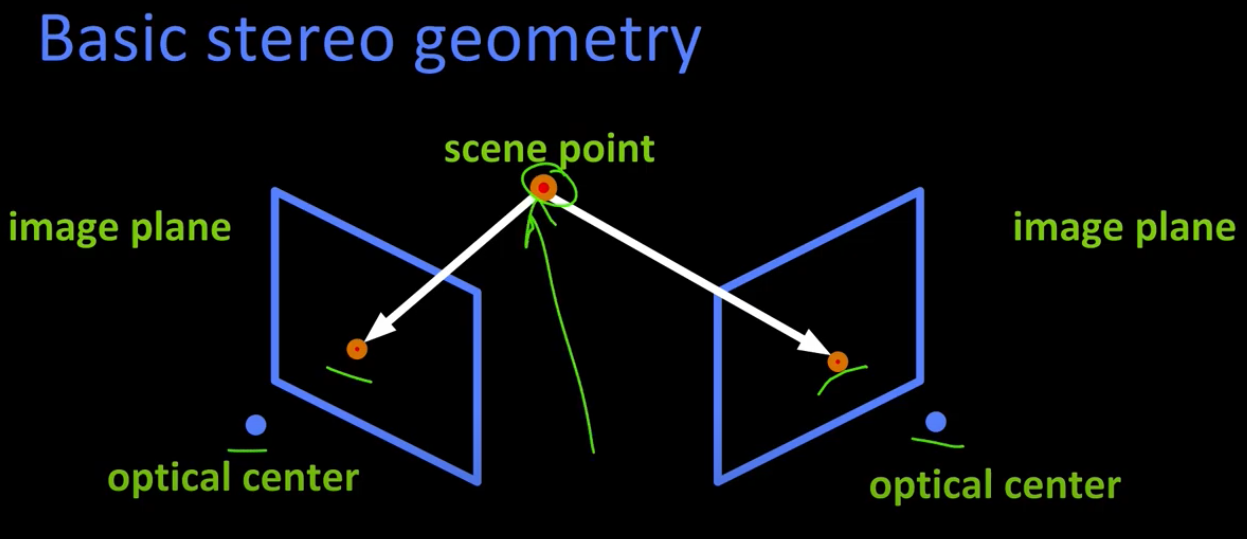
    In order to estimate the depth (the shape between 2 views) there are 2 things we have to consider:

  • The pose of cameras (so-called the camera “calibration”)
  • Image points correspondences (which point corresponds to which) - for example, this red dot on 2 images.


We are going to talk about the image points correspondence first.

Geometry for a simple stereo system

  • First, we assume the parallel optical axes, known camera parameters - or, calibrated cameras.
  • The image planes are coplanar - they are in the same plane. The schema below as we are looking down on cameras system.
  • We assume that our cameras are separated by baseline B and both cameras have a focal length f.
  • The point P is located at the distance Z in camera coordinate system. Thus, Z is a distance from point P all the way down to the center of projection.

  • Now, we can show how the point P projectes into both the left and right images.
  • X_l (positive) - the distance to the left optic axis. X_r (left) - distance to the right optic axis.



Depth from disparity



  • Since depth is distance to the object and disparity is the inverse proportional to depth, the brightest values on disparity map D(x,y) are closest to camera.
  • Disparity in a simple words - difference of X coordinates between point in left and right images.